Question

An insurance analyst working for a car insurance company would like to determine the proportion of accident claims covered by the company. A random sample of 200 claims shows that the insurance company covered 80 accident claims and did not cover 120 claims. Construct a 90 percent confidence interval estimate of the true proportion of claims covered by the insurance company.

Answer 1

0.343 < Pp < 0.457

Explanation:

We are going to denote the population proportion of claims covered as Pp.

Ps is going to be the sample proportion of claims covered by the insurance company.

Ps = 80/200 = 0.40

Qs = 1 - Ps = 0.60

n = total number of claims = 200

E is going to be the margin of error.

`E=z\sqrt{((Ps)(Qs))/(n) }`

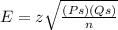
z is the critical value. The z score for a confidence level of 90 % is going to be: 1.645

`E=1.645\sqrt{((0.4)(0.6))/(200) }`

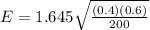
E = 0.057

The confidence interval for the population proportion is: (Ps - E, Ps + E)

(0.343, 0.457)

or

0.343 < Pp < 0.457