Question

How much thermal energy is

needed to change 3.00 x 102 g of ice at -30.0°C
to water vapor at 130.0°C?

Answer 1

Qt = 940500 [J]

Step-by-step explanation:

In order to solve this problem and understand it well, we must analyze that the ice melts or changes phase at a temperature of 0 [°c], then the water at a temperature of 100 [°C] evaporates or changes phase. That is, we have 5 different stages of water (initially in the form of ice), which are:

-) From -30 [°C] to 0 [°C] = Sensible change of temperature

-) At 0 [°C] = Latent heat of melting ice = 334 x 10³ [J/kg]

-) From 0 [°C] to 100 [°C] = Sensible change of temperature

-) At 100 [°C] = Latent heat of fusion for water = 2260 x 10³ [J/kg]

-) From 100 [°C] to 130 [°C] = Sensible change of temperature (superheating)

We can calculate the sensible heat of any process with the following expression:

`Q=m*C_(p)*(T_(f)-T_(i))`

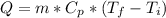
where:

Q = heat or thermal energy [J]

m = mass of the body or substance = 300 [g]

Cpw = specific heat of the water = 4180 [J/kg*°C]

Cpi = specific heat of the ice = 2090 [J/kg*°C]

Tfinal = final temperature of the process [°C]

Tinicial = initial temperature of the process [°C]

And for some latent heat process, we can calculate the thermal energy using the following expression:

`Q_(lat)=m*Dh_(fus/eva)`

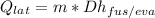
where:

Dhfus/eva = Fusion heat or latent heat [J/kg]

So, we need to calculate the fice processes.

`Q_(1)=0.3*2090*(0-(-30))\\Q_(1)=18810 [J]\\Q_(2)=0.3*334*10^(3) \\Q_(2)=100200[J]\\Q_(3)=0.3*4180*(100-0)\\Q_(3)=125400[J]\\Q_(4)=0.3*2260*10^(3)\\Q_(4)=678000[J]\\Q_(5)=0.3*2010*(130-100)\\Q_(5)=18090[J]`

And the final step is the sum of all the five heat processes.

`Q_(t)=Q_(1)+Q_(2)+Q_(3)+Q_(4)+Q_(5)\\Q_(t)=18810+100200+125400+678000+18090\\Q_(t)=940500[J]`