Answer:
The magnitude of force per
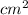 is
is
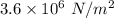
Solution:
As per the question:
Increase in the volume,

Bulk Modulus, B =
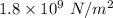
Now, to calculate the Normal Force's magnitude, F exerted by the juice:
Volume change of an elastic substance on the application of a force is given by:

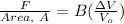
Now, putting suitable values in the above eqn:
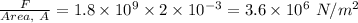
Here, F is the force exerted on the juice by the container per
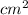 , there an equal reaction force per
, there an equal reaction force per
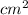 will be exerted by the juice on the container.
will be exerted by the juice on the container.