Answer:
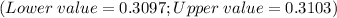 .
.
We can also represent it as
 .
.
Step-by-step explanation:
This is a case of finding two values that define an interval in which is included the population mean for the impurity in the chemical process with a probability of 95%.
We have full information to this respect to solve the question:
- The population standard deviation, which is
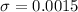 .
. - The sample mean, which is
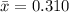 .
. - The sample size
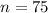 .
.
That is, we can find the 95% confidence interval for a given population standard deviation.
The formula for finding these two values, in these conditions, is as follows:
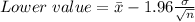 .
.
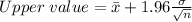 .
.
We have already confirmed that we have all these values: the population standard deviation, the sample mean and the sample size.
The number 1.96 corresponds to a z-score that is 1.96 times the standard deviation from the mean, and represents the confidence coefficient and depends on the confidence level, which is in this case of 5% (or 0.05). A confidence level of 5% determines this 95 % confidence interval.
Notice that we are going to use a mean obtained from a sample of 75 elements
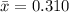 , which represents a sample mean.
, which represents a sample mean.
As a result, in order to find the two values that define the 95% confidence interval, we can proceed as follows:
Lower value of the 95% confidence interval
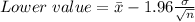 .
.
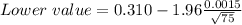 .
.
 .
.
Upper value of the 95% confidence interval
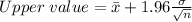 .
.
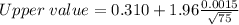 .
.
 .
.
Thus, the 95% confidence interval, or the interval for which there is a probability of 95% to find the population mean for this certain type of impurity:
 .
.
 .
.
That is:
 .
.