Question

An electron is confined to a region of size 0.15 nm (i.e., infinite potential walls at either end). (a) (5 pts) What is the ground state energy in eV? (b) (5 pts) The electron falls from the 5th excited state to the 3rd excited state, emitting a photon in the process. What is the wavelength of the photon in nm?

Answer 1

(a). The ground state energy is 16.56 eV.

(b). The wavelength of the emitted photon is 4.67 nm.

Step-by-step explanation:

Given that,

Size l= 0.15 nm

We need to calculate the ground state energy

Using formula of energy state

`E_(n)=(n^2h^2)/(8m_(e)L^2)`

For ground state,

`E_(1)=((6.6*10^(-34))^2)/(8*9.1*10^(-31)*(0.15*10^(-9))^2)`

`E_(1)=2.65*10^(-18)\ J`

`E_(1)=(2.65*10^(-18))/(1.6*10^(-19))`

`E_(1)=16.56\ ev`

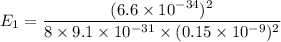
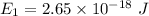
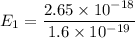
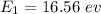
The ground state energy is 16.56 eV.

(b). We need to calculate the energy difference between 5th excited and 3rd excited state

`\Delta E=E_(5)-E_(3)`

`\Delta E=(5^2-3^2)(h^2)/(8m_(e)l^2)`

`\Delta E=16*16.56`

`\Delta E=264.96\ ev`

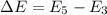
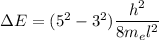
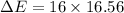
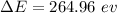
We need to calculate the wavelength of the emitted photon

Using formula of wave length

`\Delta E=(hc)/(\lambda)`

`\lambda=(hc)/(\Delta E)`

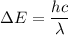
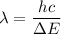
Put the value into the formula

`\lambda=(1240)/(264.96)`

`\lambda=4.67\ nm`

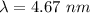
The wavelength of the emitted photon is 4.67 nm.

Hence, This is the required solution.