Question

Using a rope that will snap if the tension in it exceeds 387 N, you need to lower a bundle of old roofing material weighing 449 N from a point 6.1 m above the ground. a) What magnitude of the bundle’s acceleration will put the rope on the verge of snapping? b) At that acceleration, with what speed would the bundle hit the ground?

Answer 1

(a) 1.53
`m/s^(2)`

(b) 4.06 m

Solution:

Maximum tension,
`T_(max) = 387 N`

Weight of the material, w = 449 N

Distance from the ground, d = 6.1 m

Now,

(a) To calculate the magnitude of the acceleration of the bundle:

The mass of the bundle:

w = mg = 449

`m = (449)/(g) = (449)/(9.8) = 45.82 kg`

Now, balancing the forces:

`ma = w - T_(max)`

`a = (w - T_(max))/(m)`

`a = (449 - 387)/(45.82) = 1.353 m/s^(2)`

Now,

(b) The speed of the bundle can be calculated as:

Using the third eqn of motion:

`v'^(2) = v^(2) + 2ad`

where

v = initial velocity = 0

v' = velocity of the bundle with which it hit the ground.

`v'^(2) = 0 + 2* 1.353* 6.1 = 16.508`

`v' = √(16.508) = 4.06\ m/s`

Answer 2

a) -1.4 m/s^2

b) 4.1 m/s

Step-by-step explanation:

Tension force that must be applied on the rope is greater than 387 N

The weighing of material is 449 N

The vertical height between the bundle and the ground = 6.1 m

a)

the mass of the bundle weighing over acceleration,

F_g = ma

m= F_g/a = 449/9.8 = 45.81 Kg

the forces that act on the bundle are the tension ( for example, upward)

and the weighing force, but they are opposite to each other so,

T-mg = ma

F_g =ma

then,

T-mg = ma

so acceleration is:

a= T-mg/m = (287-45.81×9.81)/45.81 = -1.4 m/s^2

a= -1.4 m/s^2

Minus sign indicates that the acceleration in downward direction.

b) The displacement of the bundle to reach the ground is Δy =6.1 m

v^2=u^2+2aΔy

initial velocity is zero u= 0

v^2 = 2aΔy

`v= √(2*(-1.4)(-6.1))`

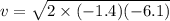
v= 4.1 m/s