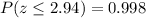Question

A marketing consultant observed 40 consecutive shoppers to estimate the average money spent by shoppers in a supermarket store. Assume that the money spent by the population of shoppers follow a Normal distribution with a standard deviation of $21.51. What is the probability that the average money spent by a sample of 40 shoppers is within $10 of the actual population mean.

Answer 1

0.998 is the probability that the average money spent by a sample of 40 shoppers is within $10 of the actual population mean.

Explanation:

We are given the following information in the question:

Standard Deviation, σ = $21.51

We are given that the distribution of average money spend is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/((\sigma)/(√(n)))`

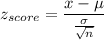
We have to find:

P( average money spent is within $10 of the actual population mean.)

`= P( z \leq \displaystyle(10* √(40))/(21.51)}) = P(z \leq 2.94)`

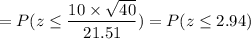
Calculation the value from standard normal z table, we have,

`P(z \leq 2.94) = 0.998`