Answer:
Explanation:
Let X be the scheduled commuting time on the shuttle "LX" from the student center to library is 15 minutes.
Suppose that the actual commuting time is uniformly distributed between 10 and 22 minutes.
X is U(10,22)
a) the probability that the commuting time will be less than 13 minutes
=
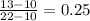
b) the probability that the commuting time will be between 12 and 18 minutes =
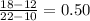
c) the expected commuting time=E(x) =
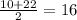
the standard deviation of the commuting time=Std dev (x) =

d) the expected commuting time be decreased if the actual commuting time is uniformly distributed between 10 and 20 minutes
New mean =
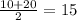
I.e. mean reduced by 1 minute.