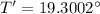Question

When resting, a person has a metabolic rate of about 3.0 105 joules per hour. The person is submerged neck-deep into a tub containing 1.21 103 kg of water at 19.30° C. If the heat from the person goes only into the water, find the water temperature after half an hour.

Answer 1

The temperature after half an hour is
`19.3002^(\circ)`

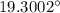
Solution:

As per the question;

Metabolic rate of the person is 3.0105 J/h

Temperature, T =
`19.30^(\circ)`

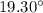
Mass of the water,
`m_(w) = 1.2103 kg`

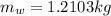
Time duration, t = 0.5 h = 30 min = 180 s

Now,

Heat,
`Q = ms\Delta t`

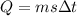
Thus heat transfer in half an hour:

`Q = 3.0105* 0.5 = 1.505 J`

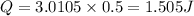
Now, the temperature of water after half an hour, T' is given by:

`Q = m_(w)s\Delta T = ms(T' - T)`

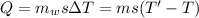
where

s = 4186 J

`1.505 = 1.21103* 4186* (T' - 19.30^(\circ))`

`T' = 19.3002 ^(\circ)`