Answer:
6,582.18
Step-by-step explanation:
this exercise can be solve by calculating the present value of each payment, and at the end substrating that sum from the initial payment, but there must be carefull because there is said to use a discount rate, so lets first remember how to calculate present and future values with discount rates:
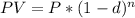
where P is the payment value, and

so applying this to the given values, we have:
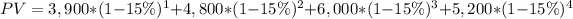
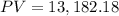
so the discounted payback is given by:
dp=13,182.18-6,600
dp=6,582.18