Question

How do the graphs of the functions differ from the graph of f(x)=3.5x^3?

For each function, select Steeper, Less steep, or Reflected over the x-axis to describe the differences between the graph of the function and the graph of f(x).
Select all answers that are correct.

Answer 1

Given:

The function is
`f(x)=3.5x^3`.

To find:

Whether the given function is Steeper, Less steep, or Reflected over the x-axis to describe the other function.

Solution:

Transformation of function: If f(x) is function and

`g(x)=a\ f(x)`

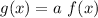
Here, a is vertical stretch or compression.

If 0<|a|<1, then g(x) is less steeper than f(x) because f(x) is vertically compressed.

If |a|>1, then g(x) is steeper than f(x) because f(x) is vertically stretched.

If a is negative, the f(x) is reflected over the x-axis, to get g(x).

On comparing the function
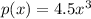`p(x)=4.5x^3` with
`f(x)=3.5x^3`, we get 4.5>3.5 So, it is the case vertical stretched and p(x) is steeper than f(x).

On comparing the function
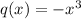`q(x)=-x^3` with
`f(x)=3.5x^3`, we get |-1|=1<3.5 So, it is the case vertical compression and q(x) is less steeper than f(x) and because of negative sign the function is reflected over axis.

On comparing the function
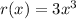`r(x)=3x^3` with
`f(x)=3.5x^3`, we get 3<3.5 So, it is the case vertical compression and r(x) is less steeper than f(x).

Therefore,
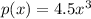`p(x)=4.5x^3` is steeper.

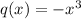`q(x)=-x^3` is less steep and reflected over the x-axis.

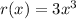`r(x)=3x^3` is less steep.