Question

Forahigh-riskdriver,thetimeindaysbetweenthe beginning of a year and an accident has an exponential pdf. Suppose an insurance company believes the probability that such a driver will be involved in an accident in the first forty days is 0.25. What is the probability that such a driver will be involved in an accident during the first seventy-five days of the year?

Answer 1

The probability that such a driver will be involved in an accident during the first seventy-five days of the year is 0.408

Explanation:

Consider the provide information.

The probability that such a driver will be involved in an accident in the first forty days is 0.25.

Therefore,
`P(X\leq 40)=0.25`

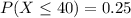
Where is X represents the random variable that shows time between beginning of a year and an accident.

X is the exponential distribution with λ as a parameter.

`P(X\leq x)=1-e^(-\lambda x), x\geq 0`

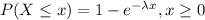
Therefore,

`P(X\leq 40)=1-e^(-40\lambda)`

`1-e^(-40\lambda)=0.25`

`e^(-40\lambda)=0.75\\-40\lambda=ln(0.75)\\\lambda=0.00719\approx0.007192`

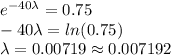
Now we want the probability that a driver will be involved in an accident during the first seventy five days.

`P(X\leq 75)=1-e^(-75* 0.0072)=0.408`

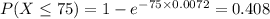
Hence, the probability that such a driver will be involved in an accident during the first seventy-five days of the year is 0.408