Answer:
4216,22 m/s
Step-by-step explanation:
Linear speed can be calculated with:
V = 2πr / T
Where V is linear speed, r is radius of the circular path which the object takes and T is period of the rotational motion. We want to calculate the speed in SI units, so:
1250 kilometers = 1250 *
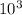 meters
meters
6400 kilometers = 6400 *
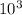 meters
meters
We will take r as the sum of radius of the Earth and height of the satellite because we need the distance between object and its centre of rotation. (Figure 1).
r= 1250 *
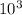 + 6400 *
+ 6400 *
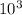 = 7650 *
= 7650 *
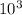 meters
meters
T=190 minutes * 60 = 11400 seconds.
We will take pi as 3.1415, let us place values to the equation:
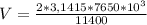
V= 4216,22 m/s