Answer:
Explanation:
Given that you and a friend play a game where you each toss a balanced coin.
If the upper faces on the coins are both tails, you win $1;
if the faces are both heads, you win $2;
if the coins do not match (one shows a head, the other a tail), you lose $1 (win (−$1)).
Let Y be the amount won
Then Y can take values as 1,2 and -1
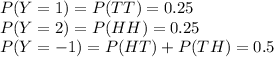
The above is the probability distribution for Y.