Answer:
the length and the width are inversely proportional to each other (
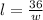 or
or
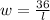 )
)
Explanation:
Let
l units = length of the rectangle,
w units = width of the rectangle.
The area of the rectangle is
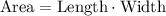
A rectangle has an area of 36 square units, so
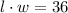
Complete the table with some values of l and w that fit the previous formula:

As you can see, the length and the width are inversely proportional to each other (
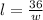 or
or
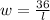 )
)