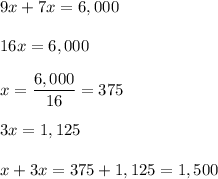Question

The school sold $6000 worth of tickets. Adult tickets were seven dollar and children’s tickets were three dollars. Three times as many children’s tickets were sold as adults. How many tickets In all were sold

Answer 1

1,500 tickets in total (375 adult tickets and 1,125 children tickets)

Explanation:

Let x be the number of adult tickets sold.

Three times as many children tickets were sold as adults, so 3x is the number of children tickets sold.

Children tickets were three dollars, so 3x children tickets cost
`\$3\cdot 3x=\$9x.`

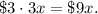
Adult tickets were seven dollar, so x adult tickets cost
`\$7\cdot x=\$7x.`

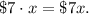
The school sold $6000 worth of tickets.

Hence,

`9x+7x=6,000\\ \\16x=6,000\\ \\x=(6,000)/(16)=375\\ \\3x=1,125\\ \\x+3x=375+1,125=1,500`