Question

Let h(x) be a function whose second derivative is h 00(x) = x 3 − 4x 2 + 5x. h(x) has critical points at x = −1, x = 0, and x = 1. Which of these points are local maxima, which are local minima, and which can you not tell just by using the second derivative test?

Answer 1

*The function has a minimum in x=-1

*The function has a maximum in x=1

*The second derivative is not enough to determine if the function has either a maximum or a minimum in x=0.

Explanation:

1. Evaluate the second derivative in the first critical point x=-1:

`h`

`h`

`h`

`h`

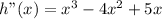
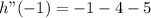
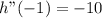
As the value is smaller than zero, the function has a minimum in x=-1

2. Evaluate the second derivative in the second critical point x=1

`h`

`h`

`h`

`h`

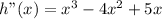
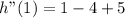
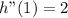
As the value is larger than zero, the function has a maximum in x=1

3. Evaluate the second derivative in the third critical point x=0

`h`

`h`

`h`

`h`

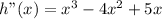
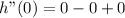
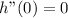
As the value is equal to zero, the second derivative is not enough to determine if the function has either a maximum or a minimum in x=0.