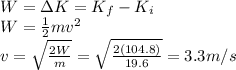Question

A luggage handler pulls a suitcase of mass 19.6 kg up a ramp inclined at an angle 24.0 ∘ above the horizontal by a force F⃗ of magnitude 152 N that acts parallel to the ramp. The coefficient of kinetic friction between the ramp and the incline is 0.264. The suitcase travels a distance 4.20 m along the ramp. The coefficient of kinetic friction between the ramp and the incline is If the suit-case travels 3.80 m along the ramp, calculate (a) the work done on the suitcase by the force (b) the work done on the suitcase by the gravitational force; (c) the work done on the suitcase by the normal force; (d) the work done on the suitcase by the friction force; (e) the total work done on the suitcase. (f) If the speed of the suitcase is zero at the bottom of the ramp, what is its speed after it has traveled 3.80 m along the ramp?

Answer 1

(a) 638.4 J

The work done by a force is given by

`W=Fd cos \theta`

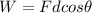
where

F is the magnitude of the force

d is the displacement of the object

`\theta` is the angle between the direction of the force and the displacement

Here we want to calculate the work done by the force F, of magnitude

F = 152 N

The displacement of the suitcase is

d = 4.20 m along the ramp

And the force is parallel to the displacement, so
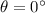`\theta=0^(\circ)`. Therefore, the work done by this force is

`W_F=(152)(4.2)(cos 0)=638.4 J`

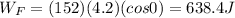
b) -328.2 J

The magnitude of the gravitational force is

W = mg

where

m = 19.6 kg is the mass of the suitcase

`g=9.8 m/s^2` is the acceleration of gravity

Substituting,

`W=(19.6)(9.8)=192.1 N`

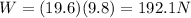
Again, the displacement is

d = 4.20 m

The gravitational force acts vertically downward, so the angle between the displacement and the force is

`\theta= 90^(\circ) - \alpha = 90+24=114^(\circ)`

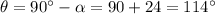
Where
`\alpha = 24^(\circ)` is the angle between the incline and the horizontal.

Therefore, the work done by gravity is

`W_g=(192.1)(4.20)(cos 114^(\circ))=-328.2 J`

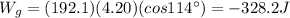
c) 0

The magnitude of the normal force is equal to the component of the weight perpendicular to the ramp, therefore:

`R=mg cos \alpha`

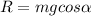
And substituting

m = 19.6 kg

g = 9.8 m/s^2

`\alpha=24^(\circ)`

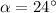
We find

`R=(19.6)(9.8)(cos 24)=175.5 N`

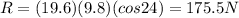
Now: the angle between the direction of the normal force and the displacement of the suitcase is 90 degrees:

`\theta=90^(\circ)`

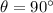
Therefore, the work done by the normal force is

`W_R=R d cos \theta =(175.4)(4.20)(cos 90)=0`

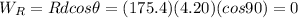
d) -194.5 J

The magnitude of the force of friction is

`F_f = \mu R`

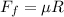
where

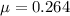`\mu = 0.264` is the coefficient of kinetic friction

R = 175.5 N is the normal force

Substituting,

`F_f = (0.264)(175.5)=46.3 N`

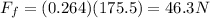
The displacement is still

d = 4.20 m

And the friction force points down along the slope, so the angle between the friction and the displacement is

`\theta=180^(\circ)`

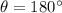
Therefore, the work done by friction is

`W_f = F_f d cos \theta =(46.3)(4.20)(cos 180)=-194.5 J`

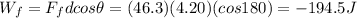
e) 115.7 J

The total work done on the suitcase is simply equal to the sum of the work done by each force,therefore:

`W=W_F + W_g + W_R +W_f = 638.4 +(-328.2)+0+(-194.5)=115.7 J`

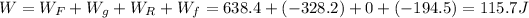
f) 3.3 m/s

First of all, we have to find the work done by each force on the suitcase while it has travelled a distance of

d = 3.80 m

Using the same procedure as in part a-d, we find:

`W_F=(152)(3.80)(cos 0)=577.6 J`

`W_g=(192.1)(3.80)(cos 114^(\circ))=-296.9 J`

`W_R=(175.4)(3.80)(cos 90)=0`

`W_f =(46.3)(3.80)(cos 180)=-175.9 J`

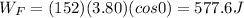
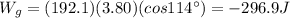
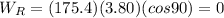
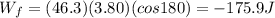
So the total work done is

`W=577.6+(-296.9)+0+(-175.9)=104.8 J`

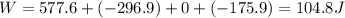
Now we can use the work-energy theorem to find the final speed of the suitcase: in fact, the total work done is equal to the gain in kinetic energy of the suitcase, therefore

`W=\Delta K = K_f - K_i\\W=(1)/(2)mv^2\\v=\sqrt{(2W)/(m)}=\sqrt{(2(104.8))/(19.6)}=3.3 m/s`