Answer:
The difference in PV between the first and the second offer, assuming an interest rate of 9% is $3,990.83
Step-by-step explanation:
Hi, first, we need to find the present value (PV) of both alternatives, the first one is as follows.
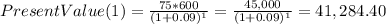
For the second alternative, the present value is as follows.
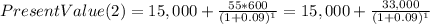
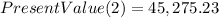
Now, the difference is:
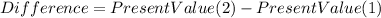
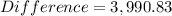
So the difference between the present value ofboth alternatives is $3,990.83 (being the lowest the first alternative)
Best of luck