Question

What is the midpoint of the segment shown below? ​

Answer 1

We conclude that the midpoint of the segment is:

• 
  `\left(-(9)/(2),\:(3)/(2)\right)`

Hence, option D is correct.

Explanation:

Given the points

• (-6, -1)

• (-3, 4)

Finding the midpoint of the segment using the formula

`\mathrm{Midpoint\:of\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad \left((x_2+x_1)/(2),\:\:(y_2+y_1)/(2)\right)`

`\left(x_1,\:y_1\right)=\left(-3,\:4\right),\:\left(x_2,\:y_2\right)=\left(-6,\:-1\right)`

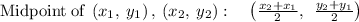
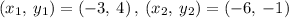
so

`=\left((-6-3)/(2),\:(-1+4)/(2)\right)`

`=\left(-(9)/(2),\:(3)/(2)\right)`

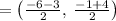
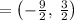
Therefore, we conclude that the midpoint of the segment is:

• 
  `\left(-(9)/(2),\:(3)/(2)\right)`

Hence, option D is correct.