Answer:
a) (8.4375,9.8425)
b) 87
Explanation:
We are given the following data-set.
11.53, 8.35, 11.66, 11.54, 9.83, 5.92, 7.14, 8.41, 8.99, 13.81, 10.53, 7.4, 6.7, 8.42, 8.4, 8.18, 9.5, 7.22, 9.87,6.52, 8.55, 9.75, 9.27, 10.61, 8.89, 10.01, 11.17, 7.62, 6.43, 9.09, 8.53, 7.91, 8.13, 7.7, 10.45, 11.3, 10.98, 8.14,11.48, 8.44, 12.52, 10.12, 8.09, 7.34
n = 44
Sample Mean = 9.14 mg per Litre
Population Standard Deviation = 2 mg per Litre
a) Formula:
Confidence interval:
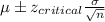
Putting the values, we get,

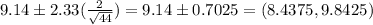
b) Thus, it could be said that above interval gives about 98% confidence that it will contain the true value of mean of the dissolved oxygen content for the warehouse.
c) Margin of error

Thus, a sample size of 87 is required to get a 98% confidence interval with error margin 0.5.