Question

Ten identical lengths of wire are laid closely

side-by-side. Their combined width is measured

and found to be 14.2 mm. Calculate:

a the radius of a single wire

b the volume in mm of a single wire if its

length is 10.0 cm (volume of a cylinder =

Tr’h, where r=radius and h= height).


Can you find b

Answer 1

• a) The radius of a single wire is 0.710 mm

• b) The volume of a single wire is 158 mm³

Step-by-step explanation:

a) Calculate the radius of a single wire

Since ten identical lengths of wire are laid closely, the combined width is equal to the sum of the diameters of the ten wires.

That is:

• 
  `Combined-width=10* diameter`

From which you can solve for the diameter of a single wire:

`14.2mm=10* diameter\\ \\ \\ diameter=14.2mm/10=1.42mm`

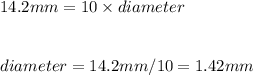
The radius is half the diameter, so:

• 
  `radius=1.42mm/2=0.710mm`

b) Calculate the volume in mm of a single wire if its length is 10.0 cm

The shape of one wire is cylindrical. So, the formula for the volume is:

• 
  `Volume=\pi * r^2* L`

Where r is the radius and L is the length.

Since the width is given in mm, conver the length to mm too.

• 
  `10.0cm* 10mm/cm=100.mm`

And subsituting the values in the formula of the volume you get:

• 
  `V=\pi * (0.710mm)^2* 100.mm=158.37mm^3`

That must be rounded to 3 significant figures: 158 mm³.