Question

In a large collection of real SMS text messages from participating cellphone users, 747 of the 5574 total messages (13.40%) are identified as spam. The word "text" (or "txt") is contained in 7.01% of all messages and in 38.55% of all spam messages. What is the probability that a message is spam, given that it contains the word "text" (or "txt")?

Answer 1

The probability that a message is spam, given that it contains the word "text", is 73.69%

Explanation:

We define the events:

A= messages are identified as spam

B= the word "text" is contained in the messages

Hence,

P(A)=13.40%

P(B)=7.01%

P(B|A)=38.55%

The conditional probability of the Bayes theorem is given by:

`P(A|B)=(P(A)P(B|A))/(P(B))`

Then,

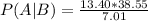`P(A|B)=(13.40*38.55)/(7.01)` =73.69%