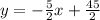Answer:
Explanation:
The slope intercept form of a line is given as:
y = mx + c
Where m is the slope and c is the y-intercept
Let's rearrange the equation given in this form:
2x - 5y = -11
5y = 2x + 11
y = 2/5 x + 11/5
So the slope is 2/5
Slope of line that is perpendicular to this is the "negative reciprocal" of this slope. Which means the slope of perpendicular line would be -5/2
Thus, equation would become: y = -5/2x + c
Now we need to find c. For this we plug in 7 into x and 5 into y and solve for c [(7,5) is the point given]. Thus,
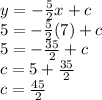
Thus, the equation of perpendicular line is: