Question

The length of time it takes to find a parking space at 9 A.M. follows a normal distribution with a mean of 7 minutes and a standard deviation of 3 minutes. Based upon the above information and numerically justified, would you be surprised if it took less than one minute to find a parking space

Answer 1

There is a 2.28% probability that it takes less than one minute to find a parking space. Since this probability is smaller than 5%, you would be surprised to find a parking space so fast.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X.

Also, a probability is unusual if it is lesser than 5%. If it is unusual, it is surprising.

In this problem:

The length of time it takes to find a parking space at 9 A.M. follows a normal distribution with a mean of 7 minutes and a standard deviation of 3 minutes, so
`\mu = 7, \sigma = 3`.

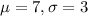We need to find the probability that it takes less than one minute to find a parking space.

So we need to find the pvalue of Z when
`X = 1`

`Z = (X - \mu)/(\sigma)`

`Z = (1 - 7)/(3)`

`Z = -2`

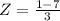
`Z = -2` has a pvalue of 0.0228.

There is a 2.28% probability that it takes less than one minute to find a parking space. Since this probability is smaller than 5%, you would be surprised to find a parking space so fast.