Answer:
3 roots are:
4, 4i, -4i
Explanation:
This is a cubic equation that has 3 roots. One root is given, we got to find the other two.
Let's group first 2 terms and last two terms and factor and solve:
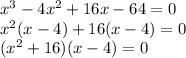
From here we can say:
x^2 + 16 = 0
and
x - 4 = 0 [x = 4, we already know this solution]
Let's find the other 2 roots from the 1st equation:

Note:
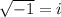
So the 3 roots are:
4, 4i, -4i