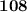Answer:
Simplifying the expression
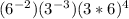 we get
we get
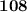
Explanation:
We need to simplify the expression
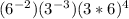
Solving:
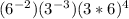
Applying exponent rule:
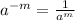
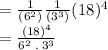
Factors of
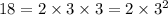
Factors of
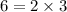
Replacing terms with factors
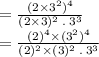
Using exponent rule:
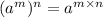
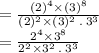
Using exponent rule:
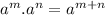
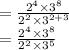
Now using exponent rule:
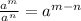
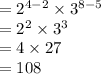
So, simplifying the expression
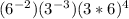 we get
we get