Question

g Georgianna claims that in a small city renowned for its music school, the average child takes at least 5 years of piano lessons. We have a random sample of 20 children from the city, with a mean of 4.6 years of piano lessons and a standard deviation of 2.2 years. What is the 90% confidence interval for the average number of years students take piano lessons in this city? Group of answer choices

Answer 1

[3.75 years, 5.45 years]

Explanation:

The 90% confidence interval is given by the interval

`\large [\bar x-t^*(s)/(\sqrt n), \bar x+t^*(s)/(\sqrt n)]`

where

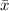`\large \bar x` is the sample mean

s is the sample standard deviation

n is the sample size

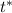`\large t^*` is the 0.05 (5%) both-sided (**) critical value for the Student's t-distribution with 19 degrees of freedom (sample size -1), which is an approximation to the Normal distribution for small samples (n≤ 30).

Either by using a table or the computer, we find

`\large t^*= 1.729`

and our 90% confidence interval is

`\large [4.6-1.729*(2.2)/(√(20)), 4.6+1.729*(2.2)/(√(20))]=\boxed{[3.75,5.45]}`

(**) 5% of the area to the left of
`\large  -t^*` and 5% to right of
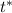`\large t^*` for a total of 90% inside the interval
`\large [-t^*,+t^*]`