Answer:
Some few inverse variation formulae are given below.
Explanation:
If y varies inversely as x, then we can write the relation:
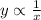
When we introduce the constant of proportionality we get:
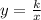
Or
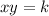
The constant k is referred to as the constant of variation or constant of proportionality.
Similarly, if y varies inversely as the square of x, then the formula for y becomes:
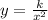
Also
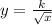
is also an inverse variation formula for y.
etc
I hope this explanation will help you answer the complete question.