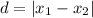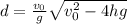Question

A cannon placed at the origin fires a projectile with velocity ~v0, which passes during its trajectory through two points both a distance h above the horizontal, before landing. Show that if the cannon is adjusted for maximum range and air resistance is neglected, then the separation of the two points is d = v0 g p v 2 0 − 4gh.

Answer 1

The equations for the y position of the trajectory is:

`y=sin\phi v_0t-(1)/(2)gt^2`

The range is of the trajectory is reached at y = 0:

`sin\phi v_0t-(1)/(2)gt^2 = 0`

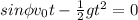
Solving for time t:

`t=(2sin\phi v_0)/(g)`

The x position of the trajectory is given by:

`x=cos\phi v_0t`

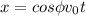
Combining the equations we get the function:

`x=(2sin\phi cos\phi v_0^2)/(g)=sin(2\phi)(v_0^2)/(g)`

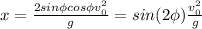
Taking the derivative and setting it to zero:

`(dx)/(d\phi)=2cos(2\phi)(v_0^2)/(g)= 0`

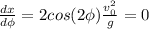
Find the maximum angle:

`\phi=45`

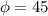
Using this solution to find the trajectory in terms of x and y and setting it equal to height h:

`y=(sin45 v_0)/(cos45v_0)x-(g)/(2cos^245v_0^2)x^2=x-(g)/(v_0^2)x^2=h`

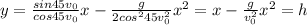
Normalize:

`x^2-(v_0^2)/(g)x+(hv_0^2)/(g)=0`

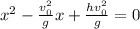
Use quadratic formula:

`x_(1/2)=(v_0^2)/(2g)+/-v_0\sqrt{(v_0^2-4hg)/(4g^2)}`

The distance is the difference between the two points:

`d=|x_1-x_2|`

`d=(v_0)/(g) √(v_0^2-4hg)`