Question

I need help w/ this!! thank you

Answer 1

`\boxed{\pink{\sf \leadsto Yes \ there \ is \ a \ solution \ of \ the \ given \ inequality .}}`

Explanation:

A inequality is given to us and we need to convert it into standard form and see whether if it has a solution . So let's solve the inequality.

The inequality given to us is :-

`\bf\implies |2y + 3 | - 1 \leq 0 \\\\\bf\implies |2y+3|\leq 1 \\\\\bf\implies (|2y+3|)^2 \leq 1^2 \\\\\bf\implies (2y+3)^2 \leq 1 \\\\\bf\implies (2y)^2+3^2+2(2y)(3) \leq 1 \\\\\bf\implies 4y^2+9+12y - 1 \leq 0 \\\\\bf\implies 4y^2+12y+8 \leq 0 \\\\\bf\implies 4( y^2 + 3y + 2 ) \leq 0 \\\\\bf\implies y^2+3y +2 \leq 0 \:\:\bigg\lgroup \purple{\bf Standard \ form \ of \ inequality }\bigg\rgroup \\\\\bf\implies y^2y+2y+y+2 \leq 0 \\\\\bf\implies y(y+2)+1(y+2)\leq 0 \\\\\bf\implies ( y+2)(y+1)\leq 0 \\\\\bf\implies \boxed{\red{\bf y \leq (-2) , (-1) }}`

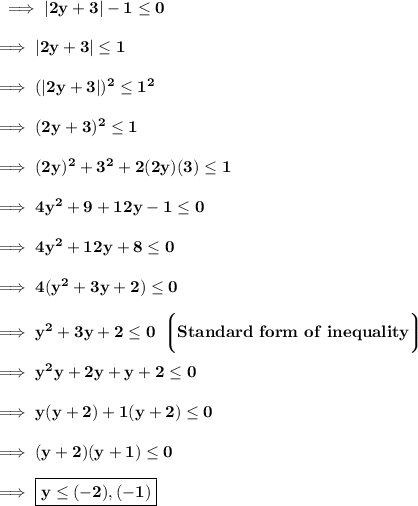
Let's plot a graph to see its interval . Graph attached in attachment .

Now we can see that the Interval notation of would be ,

`\boxed{\boxed{\orange \tt \purple{\leadsto}y \in [-2,-1] }}`

Hence the standard form of inequality is y²+3y +2 ≤ 0 and the Solution set of the inequality is [ -2 , -1 ] .