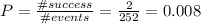Question

10 kids are randomly grouped into an A team with five kids and a B team with five kids. Each grouping is equally likely. (a) What is the size of the sample space? (b) There are two kids in the group, Alex and his best friend Jose. What is the probability that Alex and Jose end up on the same team? (c) If the group consists of five girls and five boys, what is the probability that all the girls end up on the same team?

Answer 1

a) The size of the sample space is 252.

b) P=0.444

c) P=0.008

Explanation:

a) The sample space is the set of total possible outcomes for this grouping.

In this case we have a combination of 10 elements in groups of 5 elements.

The size of the sample space is then:

`S=(n!)/(r!(n-r)!)=(10!)/(2!8!)=(3628800)/(14400)=252`

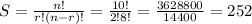
b) If Alex and Jose are in the same team, there are 3 places left in the group that can be filled by any of the other 8 kids.

If we calculate the possible combinations of 8 kids in 3 places we have:

`S_2=(n!)/(r!(n-r)!)=(8!)/(3!5!)=56`

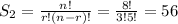
There are 56 combinations for group A which have Alex and Jose.

But if in group A neither Alex or Jose are members, both are also in the same team (group B). We can calculate this as a combination of 8 kids (everybody but Alex and Jose) in a group of 5:

`S_2=(n!)/(r!(n-r)!)=(8!)/(5!3!)=56`

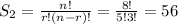
This are also 56 combinations of both kids being in Group B, as expected.

Then we can calculate the probability of both being in the same team as:

`P=(\#success)/(\#events)=(56+56)/(252)=(112)/(252)=0.444`

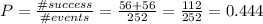
c) If there are five girls and five boys, there are only 2 combinations that have girls on the same team (one is if all the boys are in Team A, and the other is if all girls are in Team A).

Then the probability of having all five girls in one team is:

`P=(\#success)/(\#events)=(2)/(252)=0.008`