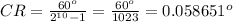Question

8.23 A TLR robot has a rotational joint (type R) whose output link is connected to the wrist assembly. Considering the design of this joint only, the output link is 600 mm long, and the total range of rotation of the joint is 40. The spatial resolution of this joint is expressed as a linear measure at the wrist, and is specified to be 0.5 mm. It is known that the mechanical inaccuracies in the joint result in an error of 0.018 rotation, and it is assumed that the output link is perfectly rigid so as to cause no additional errors due to deflection. (a) Determine the minimum number of bits required in the robot's control memory in order to obtain the spatial resolution specified. (b) With the given level of mechanical error in the joint, show that it is possible to achieve the spatial resolution specified.

Answer 1

(a) 10 bits

(b)
`0.058651^(o)`

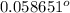
Step-by-step explanation:

The control resolution CR is calculated using

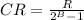`CR= \frac {R}{2^(B)-1}` where B is storage capacity and R is the range of robot

Therefore, CR of robot

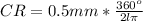`CR=0.5mm* \frac {360^(o)}{2l \pi}` Where l represents length of output link

Since l is given as 600mm

`CR=0.5mm* \frac {360^(o)}{2*600* \pi}=0.0477465^(o)`

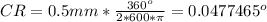
Substituting the above value of CR into the first equation

`0.0477465^(o)= \frac {40^(o)}{2^(B)-1}`

`2^(B)= 837.75804+1=838.75804`

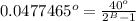
B ln 2=ln 838.75804

B=ln (838.75804)/(ln 2)= 9.712110882

B=10 bits (approximately)

(b)

From the initial equation
`CR= \frac {R}{2^(B)-1}`

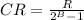
We substituate B for 10 hence

`CR= \frac {60^(o)}{2^(10)-1}= \frac {60^(o)}{1023}=0.058651^(o)`