Question

Ramon wants to plant cucumbers and tomatoes in his garden. He has room for

16
plants, and he wants to plant
3
times as many cucumbers as tomatoes. How many cucumbers and how many tomatoes should he plant?

Answer 1

The correct answer is he should plant 12 cucumbers and 4 tomatoes.

Explanation:

First we must start by analyzing the information we have:

We know that in total Ramon can only plant 16 plants.

We know that the amount of cucumbers he wants to plant is 3 times greater than the amount of tomatoes.

But what we don't know is the amount of tomatoes that he is going to plant, and that is what we are going to find out.

As we do not know this number, we will assign the incognita x.

So:

Total: 16

Number of cucumbers 3 times greater than tomatoes: 3x

Tomatoes: x

Now we just have to put together the equation:

`x + 3 x = 16`

Now we just have to solve to determine the amount of tomatoes :

`4 x = 16\\x= 16 : 4\\x= 4`

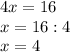
Knowing that the number of tomatoes is 4, we should only subtract that number from the total number of plants that Ramon can plant, and so we will obtain the amount of cucumbers:

16 - 4 = 12

In this way we can say that the correct answer is he should plant 12 cucumbers and 4 tomatoes.

Answer 2

Number of Cucumbers = 12

Number of Tomatoes = 4

Explanation:

Let number of cucumber be c and number of tomatoes be t

Since he has room for 16 plants, we can write:

c + t = 16

He wants to plant 3 times as many cucumbers as tomatoes. We can write:

c = 3t

We can substitute this in 1st equation and solve for t:

c + t = 16

3t + t = 16

4t = 16

t = 16/4 = 4

And c = 3t

c = 3(4) = 12

Number of Cucumbers = 12

Number of Tomatoes = 4