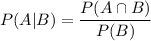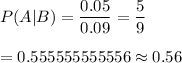Question

Of the drivers who stop at a gas station, 91% purchase gasoline, and 5% purchase both gasoline and oil. A total of 9% purchase oil. (a) What is the probability that a driver purchases oil, given that he or she purchases gasoline? Round your answer to 2 decimal places. (b) What is the probability that a driver purchases gasoline, given that he or she purchases oil? Round your answer to 2 decimal places.

Answer 1

Answer: a) 0.05

b) 0.56

Explanation:

Let A be denote the event that gas station purchase gasoline.

B be denote the event that gas station purchase oil.

As per given description, we have

P(A)-0.91 , P(B)= 0.09 , P(A ∩B)=0.05

Then, the probability that a driver purchases oil, given that he or she purchases gasoline will be :-

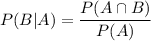`P(B|A)=(P(A\cap B ))/(P(A))` [Conditional probability formula.]

`P(B|A)=(0.05)/(0.91)=(5)/(91)\\\\=0.0549450549451\approx0.05`

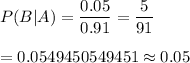
Similarly , The probability that a driver purchases gasoline, given that he or she purchases oil will be :-

`P(A|B)=(P(A\cap B ))/(P(B))`

`P(A|B)=(0.05)/(0.09)=(5)/(9)\\\\=0.555555555556\approx0.56`