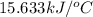Answer : The heat capacity of the bomb calorimeter
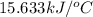
Explanation :
First we have to calculate the heat released by the combustion.
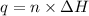
where,
q = heat released by combustion = ?
n = moles of benzoic acid =
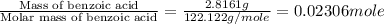
 = enthalpy of combustion = 3226.7 kJ/mole
= enthalpy of combustion = 3226.7 kJ/mole
Now put all the given values in the above formula, get:
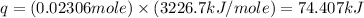
Now we have to calculate the heat capacity of the bomb calorimeter.
Heat released by the reaction = Heat absorbed by the calorimeter + Heat absorbed by the water
![q=[q_1+q_2]](https://img.qammunity.org/2020/formulas/chemistry/college/3yqkquw9xt0urtwyu8qfu9kf65yvlx00r8.png)
![q=[c_1* \Delta T+m_2* c_2* \Delta T]](https://img.qammunity.org/2020/formulas/chemistry/college/z4j1tykfisn6ks4ttchepg3letm6np6k8o.png)
where,
q = heat released by the reaction = 74.4077 kJ = 74407.7 J
 = heat absorbed by the calorimeter
= heat absorbed by the calorimeter
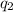 = heat absorbed by the water
= heat absorbed by the water
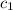 = specific heat of calorimeter = ?
= specific heat of calorimeter = ?
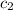 = specific heat of water =
= specific heat of water =
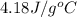
 = mass of water = 2550 g
= mass of water = 2550 g
 = change in temperature =
= change in temperature =
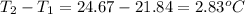
Now put all the given values in the above formula, we get:
![74407J=[(c_1* 2.83^oC)+(2550g* 4.18J/g^oC* 2.83^oC)]](https://img.qammunity.org/2020/formulas/chemistry/college/j39l79s3ab1lneh1cchhlbeiojj8qc0bs5.png)
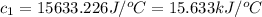
Therefore, the heat capacity of the bomb calorimeter