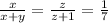Answer:

Explanation:
Given
sunny day speed= s mph
Rainy day speed=s+1 mph
Derek average speed =2.8 miles/hr
s<2.8<s+1
so on sunny day speed must be 2 mph
and on rainy day speed must be 3 mph
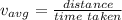
Let x be the distance traveled in sunny and y be the distance traveled in rainy weather
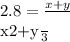
Let
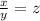
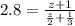
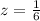
Fraction of distance traveled on sunny weather