Step-by-step explanation: Since a flying disk is the same shape as a circle, we can find the area of the flying disk by using the formula for the area of a circle.
To find the area of a circle, start with the formula for the area of a circle.
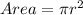
Notice that the flying disk has a radius of 7.6 centimeters so we can plug 7.6 in for the radius in our formula.
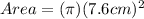
Squaring a number just means multiplying the number by itself. In this case, 7.6 cm squared is equal to 7.6 cm × 7.6 cm or 57.56 cm².
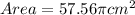
Now, remember that pi is equal to approximately 3.14 so we can estimate the area of the circle by plugging in 3.14 for pi.
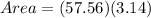
Area = 180.7384 cm²