Question

The temperature distribution across a wall 1 m thick at a certain instant of time is T(x) = a + bx + cx^2, where T is in Kelvin and x is in meters, a = 350 K, b = -100 K/m, and c = 50 K/m2. The wall has a thermal conductivity of 2 W/m·K. (a) On a unit surface area basis, determine the rate of heat transfer into and out of the wall and the rate of change of energy stored by the wall. (b) If the cold surface is exposed to a fluid at 10 °C, what is the convection coefficient?

Answer 1

a)In Q= - 200 W

Out Q = 0 W

b)h = 2.89 W/m²·K

Step-by-step explanation:

T(x) = a + bx + cx²

T(x) = 350 -100 x + 50 x²

`(dT)/(dx) = -100 + 100 x`

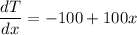
a)

We know that

`Q=-K(dT)/(dx)`

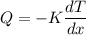
In condition : x= 0

`(dT)/(dx) = -100 + 100 x`

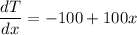
Put x= 0

`(dT)/(dx) = -100`

`Q=-K(dT)/(dx)`

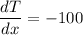
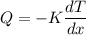
K= 2 W/m·K

Q = -100 x 2 = - 200 W

Exit condition : x= 1

`(dT)/(dx) = -100 + 100 x`

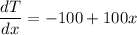
Put x= 1

`(dT)/(dx) = -100 + 100* 1`

`(dT)/(dx) = 0`

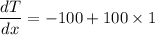
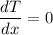
It means that right side of wall is insulated.

b)

Lets take h is the convection coefficient of fluid

Q= h ΔT

T(x) = 350 -100 x + 50 x²

At x = 0 , T= 350 K

So

ΔT = 350 - (273+10) = 350 - 283 K

ΔT = 67 K

Q= h ΔT

200 = h x 67

h = 2.89 W/m²·K