Question

) The potential difference between the plates of a capacitor is 400 V. (a) If the spacing between the plates is doubled without altering the charge on the plates, what is the new potential difference? (b) If the plate spacing is double while the voltage is held constant, by what factor will the charge change?

Answer 1

(a) 800 V

The capacitance of a parallel-plate capacitor is given by

`C=(\epsilon_0 A)/(d)`

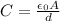
where

`\epsilon_0` is the vacuum permittivity

A is the area of each plate

d is the separation between the plates

We see that the capacitance is inversely proportional to the separation, d: in this problem, the separation between the plates is doubled (2d), so the capacitance will become half of its original value:

`C'=(C)/(2)`

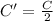
The potential difference between the plates is related to the capacitance by

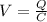`V=(Q)/(C)` (1)

where Q is the charge stored on the plate. In this problem, the charge is not changed: therefore, the new potential difference is

`V'=(Q)/(C/2)=2(Q)/(C)=2V`

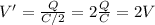
So, the potential difference has doubled, and since the initial value was

V = 400 V

The new value is

V' = 2(400) = 800 V

(b) The charge will decrease by a factor 2

As before, the plate spacing is doubled, so according to the equation

`C=(\epsilon_0 A)/(d)`

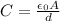
Then the capacitance is halved again:

`C'=(C)/(2)`

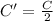
This time, however, the voltage is held constant. We can rewrite the eq.(1) as

Q = CV

And since V has not changed, we can find what is the new charge stored in the capacitor:

`Q' = C'V=(C)/(2)V=(1)/(2)(CV) = (1)/(2)Q`

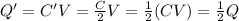
So, the charge will be halved compared to the original charge.