Question

If MNP - TSR and NQ and SU are angle bisectors, find TS.

MN = 2
TS = n + 2
NP = 3
SU = 1
NQ = n + 3

Answer 1

TS is 1

Explanation:

The given parameters are;

ΔMNP is similar to ΔTSR

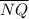`\overline {NQ}` and
`\overline {SU}` are angle bisectors of ∠MNP and ∠TSR respectively

MN = 2, TS = n + 2, NP = 3, SU = 1, NQ = n + 3

We have;

MN and TS are corresponding sides

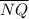`\overline {NQ}` and
`\overline {SU}` are corresponding sides

Therefore, we have;

MN/TS =
`\overline {NQ}`/
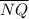`\overline {SU}` which gives;

2/(n + 2) = (n + 3)/1

(n + 2)·(n + 3) = 2

n² + 3·n + 2·n + 6 = 2

∴ n² + 5·n + 4 = 0, which gives, by factorization;

(n + 1)·(n + 4) = 0

∴ n - 1 or n = -4

TS = n + 2

When n = -1 TS = -1 + 2 = 1

When n = -4, TS = -4 + 1 = -3

Therefore, for a natural number value, we have, n = -1 and TS = 1.