Question

Pilots of high-performance fighter planes can be subjected to large centripetal accelerations during high-speed turns. Because of these accelerations, the pilots are subjected to forces that can be much greater than their body weight, leading to an accumulation of blood in the abdomen and legs. As a result, the brain becomes starved for blood, and the pilot can lose consciousness ("black out"). The pilots wear "anti-G suits" to help keep the blood from draining out of the brain. To appreciate the forces that a fighter pilot must endure, consider the magnitude of the normal force that the pilot's seat exerts on him at the bottom of a dive. The plane is traveling at 216 m/s on a vertical circle of radius 723 m. Determine the ratio of the normal force to the magnitude of the pilot's weight. For comparison, note that black-out can occur for ratios as small as 2 if the pilot is not wearing an anti-G suit.

Answer 1

Ratio is 7.58

Step-by-step explanation:

At the bottom of the circle, the net force is given by

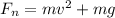`F_(n)=mv^(2)+mg` where m is mass of plane, v is the speed of plane, r is vertical circle radius

`F_(n)=m(v^(2)+g)`

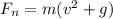
Since W=mg, dividing left side by W and right side by mg we obtain

`\frac {F_(n)}{W}= \frac {m(v^(2)+g)}{mg}`

`\frac {F_(n)}{W}=g(g+\frac {v^(2)}{r})`

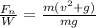
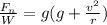
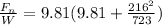`\frac {F_(n)}{W}=9.81(9.81+\frac {216^(2)}{723})`=7.578096

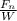`\frac {F_(n)}{W}`=7.58

Considering that
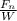`\frac {F_(n)}{W}`=7.58 which is greater than 2, the pilot is advised to wear the anti-G suit