Question

Select all the correct answers.

Which values are included in the solution set of this inequality?
2.12 – 1 > 61
I = -4
I = 3
0 1 = 1
o = 5
O r = -2

Answer 1

Option A, Option D and Option E are correct options.

Explanation:

We need to find solutions of the inequality:
`2x^2-1>6x`

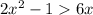
We will check the options and see, which options satisfy the inequality.

Option A

x=-4

Put x=-4

`2x^2-1>6x\\2(-4)^2-1>6(-4)\\2(16)-1>-24\\32-1>-24\\31>-24\:\:True`

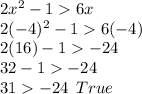
So, x=-4 is the solution of inequality.

Option B

x=3

Put x=-3

`2x^2-1>6x\\2(3)^2-1>6(3)\\2(9)-1>18\\18-1>18\\17>18\:\:False`

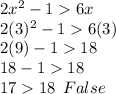
So, x=3 is not the solution of inequality.

Option C

x=1

Put x=1

`2x^2-1>6x\\2(1)^2-1>6(1)\\2(1)-1>6\\2-1>6\\1>6\:\:False`

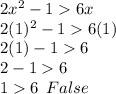
So, x=1 is not the solution of inequality.

Option D

x=5

Put x=5

`2x^2-1>6x\\2(5)^2-1>6(5)\\2(25)-1>30\\50-1>30\\49>30\:\:True`

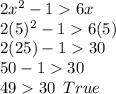
So, x=5 is the solution of inequality.

Option E

x=-2

Put x=-2

`2x^2-1>6x\\2(-2)^2-1>6(-2)\\2(4)-1>-12\\8-1>-12\\7>-12\:\:True`

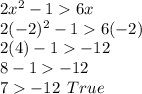
So, x=-2 is the solution of inequality.

So, Option A, Option D and Option E are correct options.