Answer:
79.81% probability of winning.
Explanation:
For each ticket, there are only two possible outcomes. Either you win, or you do not. The probability of winning in a ticket is independent of other tickets. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
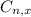 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
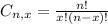
And p is the probability of X happening.
The odds of winning the prize is 1 : 53
This means that
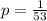
If I purchased 84 tickets what are the odds of winning in percentage.
To win, at least one of the tickets must have the prize, of 84 tickets, so
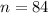 .
.
We have to find
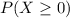 , which is given by:
, which is given by:
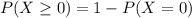
In which
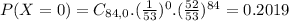
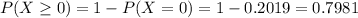
79.81% probability of winning.