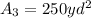Question

This question has three parts. Answer the parts in order.

An enclosed field is made up of three sections:


• One section is a 10-yard by 10-yard square.


• Another section is a larger square.


• A third section is rectangular with a width of 10 yards. It shares a side with the larger square.


The total area of the enclosed field is 975 square yards.

Part 1


What is the area, in square yards, of the smallest section? (Use only the digits 0 – 9 to enter a number.)

Part 2


What is the area, in square yards, of the largest section? (Use only the digits 0 – 9 to enter a number.)

Part 3


What is the area, in square yards, of the remaining section? (Use only the digits 0 – 9 to enter a number.)

Answer 1

The area of the smallest section is
`A_(1)=100yd^(2)`

The area of the largest section is
`A_(2)=625yd^(2)`

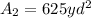
The area of the remaining section is
`A_(3)=250yd^(2)`

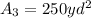
Explanation:

Please see the picture below.

1. First we are going to name the side of the larger square as x.

As the third section shares a side with the larger square and the four sides of a square are equal, we have the following:

- Area of the first section:

`A_(1)=10yd*10yd`

`A_(1)=100yd^(2)`

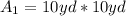
- Area of the second section:

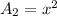`A_(2)=x^(2)` (Eq.1)

- Area of the third section:

`A_(3)=width*length`

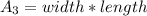
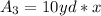`A_(3)=10yd*x` (Eq.2)

2. The problem says that the total area of the enclosed field is 975 square yards, and looking at the picture below, we have:

`A_(1)+A_(2)+A_(3)=975yd^(2)`

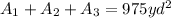
Replacing values:

`100+x^(2)+10x=975`

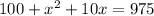
Solving for x:

`x^(2)+10x-875=0`

`x=(-10+√(100+(4*875)))/(2)`

`x=(-10+√(3600))/(2)`

`x=(-10+60)/(2)`

`x=25`

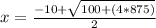
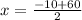
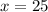
3. Replacing the value of x in Eq.1 and Eq.2:

- From Eq.1:

`A_(2)=25^(2)`

`A_(2)=625yd^(2)`

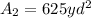
- From Eq.2:

`A_(3)=10*25`

`A_(3)=250yd^(2)`