Question

Billy-Do-Right sees an elephant dart into the road 75m ahead of his car while driving 23.6m/a. He slams on the brakes, which accelerates the car at -6.3m/s. Will he be able to avoid hitting the elephant

Answer 1

He will be able to avoid hitting the elephant

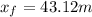`x_(f) = 43.12m` a time of t=3.7 s

Step-by-step explanation:

`x_(f1) = 75m`

`v=23.6 (m)/(s) \\a=-6.3 (m)/(s^(2) )`

`v_(f)=v_(o)+a*t\\v_(f)=0 \\t=-(v_(o))/(a)\\t=-(23.6 (m)/(s) )/(-6.3(m)/(s^(2) ) )\\t=3.7 s`

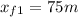
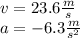
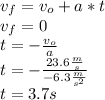
So calculated the final distance using that time to know if avoid the elephant the distance has to be less that 75m

`x_(f) = x_(o) +v_(o)*t +(1)/(2)*a*t^(2)\\x_(f) = 0m +23.6*3.7 +(1)/(2)*-6.3*3.7^(2)\\x_(f) = (87.32-44.2)m\\x_(f) = 43.12m`

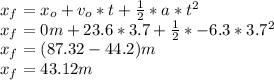
So the distance is less so he can avoid the elephant