Question

Two aqueous sulfuric acid solutions containing 20.0 wt% H2SO4

(SG = 1.139) and 60.0 wt% H2SO4 (SG = 1.498) are mixed to form a


4.00 molar solution (SG = 1.213). Taking 100kg of the 20% feed


solution as a basis, calculate the feed ratio (liters 20%


solution/liter 60% solution).

Answer 1

The feed ratio (liters 20% solution/liter 60% solution) is 3,08

Step-by-step explanation:

In this problem you have a 20,0 wt% H₂SO₄ and a 60,0 wt% H₂SO₄ solutions.

100 kg of 20% solution are 100kg/1,139 kg/L = 87,8 L

100kg×20wt% = 20 kg H₂SO₄. In moles:

20 kg H₂SO₄ × (1 kmol/98,08 kg) = 0,2039 kmol H₂SO₄≡ 203,9 mol

The final molarity 4,00M comes from:

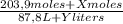`(203,9 moles+ Xmoles)/(87,8L + Yliters)` (1)

Where X moles and Y liters comes from 60,0 wt% H₂SO₄

100 L of 60,0 wt% H₂SO₄ are:

100L×
`(1,498 kgsolution)/(L)`×
`(60 kg H_(2)SO_(4))/(100kgSolution)`×
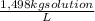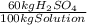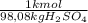`(1kmol)/(98,08kg H_(2)SO_(4))` = 0,9164 kmolH₂SO₄ ≡ 916,4 moles

That means:

X/Y = 916,4/100 = 9,164 (2)

Replacing (2) in (1):

Y(liters of 60,0 wt% H₂SO₄) = 28,52 L

Thus, feed ratio (liters 20% solution/liter 60% solution):

87,8L/28,52L = 3,08

I hope it helps!