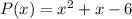Question

Find a quadratic polynomial the sum and product of whose zeroes are -3 and 2 respectively​

Answer 1

`P(x)=x^2+x-6`

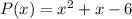
Explanation:

Quadratic Polynomial

Assume we have a polynomial factored as:

P(x)=a(x-m)(x-n)

Where m and n are the zeros of P(x).

Operating:

`P(x)=a(x^2-(m+n)x+mn)`

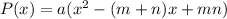
Note the coefficient of x is the negative sum of the zeros and the independent term is the product of the zeros.

If we are given the zeros m=-3 and n=2, then:

`P(x)=a(x^2-(-3+2)x+(-3)(2))`

`P(x)=a(x^2+x-6)`

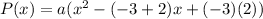
We can choose any value for a, for example, a=2:

`P(x)=2x^2+2x-12`

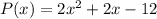
For a=1:

`P(x)=x^2+x-6`