Question

A consumer information website claims that the average price of all routers is $80. If we assume that the population standard deviation of prices is $28 (i.e., if we assume Marias sample standard deviation is a good estimate of σ), what is the probability that a random sample of 75 routers would have an average price of less than or equal to $74? Give your answer to three decimal places.

Answer 1

Answer: 0.031

Explanation:

As considering the given information, we have

`\mu=80`

`\sigma=28`

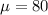
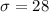
n= 75

Let x be the random variable that represents the price of all routers.

We assume that the price of all routers are normally distributed.

Z-score corresponding to x=74 will be :-

`z=(x-\mu)/((\sigma)/(√(n)))`

`z=(74-80)/((28)/(√(75)))\\\\=-1.8557687224\approx-1.86`

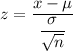
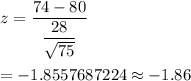
Using z-value table,

P-value = P(x ≤ -1.86)=1-P(x≤ 1.86)=1-0.9685572=0.0314428≈0.031

Hence, the required probability = 0.031