Question

The Ohio Department of Agriculture tested 203 fuel samples across the state in 1999 for accuracy of the reported octane level. For premium grade, 14 out of 105 samples failed. (They did not meet the ASTM specification and the FTC octane posting rule.) How many samples would be needed to create a 99 percent confidence interval that is within 0.02 of the true proportion of premium grade fuel-quality failures?

Answer 1

The Sample size is 1918.89035

Explanation:

Consider the provided information.

It is given that 14 out of 105 samples failed.

Therefore p = 14/105 = 0.13 3... and q=1-0.133=0.867

Samples would be needed to create a 99 percent confidence interval.

Subtract the confidence level from 1, then divide by two.

`((1 -0.99))/(2)=0.005`

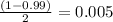
By standard normal table z=2.5758≈2.58

Calculate the sample size as:

`n=(z^2pq)/(e^2)`

Where, e is the margin of error,

Substitute the respective values.

`n=((2.58)^2(0.133)(0.867))/((0.02)^2)=1918.89`

Hence, the Sample size is 1918.89035